গণিত এ সংখ্যা আবিষ্কারের ইতিহাস ও সংখ্যার সাহায্যে গণনা

গণনার থেকেই বর্তমান গণিতের জন্ম । অতি প্রাচীন প্রস্তর যুগে আদিম মানুষ যখন গুহাবাসী ছিল , তখনও সম্ভবতঃ এক – দুই পর্যন্ত গণনা প্রচলিত ছিল । হয়ত সে যুগে পারিবারিক ও সামাজিক জীবনই ভাল করে আরম্ভ হয়নি ; তবু পদার্থের রূপ সম্বন্ধে ধারণা যে নিশ্চয়ই ছিল , তার নিদর্শন পাওয়া গেছে অনুমান পনর হাজার বছর আগেকার স্পেন ও ফ্রান্সের গুহাগাত্রে অঙ্কিত চিত্র এবং স্থানে স্থানে রক্ষিত দ্রব্য সামগ্রী আর মূর্তি থেকে । নতুন প্রস্তর যুগে মানুষ খাদ্য ‘ আহরণ ‘ থেকে ‘ উৎপাদন আরম্ভ করল ।

গণিত এ সংখ্যা আবিষ্কারের ইতিহাস

সে প্রায় দশ হাজার বছর আগেকার কথা এই যুগের মৃৎ শিল্প , কান্ঠ শিল্প ও বয়ন শিল্পের অনেক নমুনা ভূগর্ভে প্রোথিত রয়েছে । তার কতকগুলো মাটি খুঁড়ে বের করা হয়েছে । এসব থেকে দেখা যায় , তখনই গ্রাম্য সমাজ স্থাপিত হয়ে গেছে , ধানের বা গমের গোলা , রুটি সেঁকবার উনুন কুমোরের চাকা , গাড়ীর চাকা , নৌকা এবং আবাসগৃহ নির্মাণ শুরু হয়েছে ; কিন্তু এসব ছিল স্থানিক বৈশিষ্ট্য । এক স্থানে কোনও কিছু উদ্ভাবিত হলেও সে সংবাদ সহজে অন্যত্র পৌঁছতে পারত না উদাহরণস্বরূপ বলা যায় , আমেরিকার আদিম অধিবাসীরা ইউরোপের সাদা আদমি দেখবার আগে কোনও দিন গাড়ীর ঢাকা দেখেনি । তবু প্রাচীন প্রস্তর যুগের চেয়ে নতুন প্রস্তর যুগের লোক অনেক দ্রুতগতিতে উন্নতির পথে অগ্রসর হয়েছে ।  একালে গ্রামগুলোর মধ্যে পণ্যের আদান – প্রদান আরম্ভ হয়ে গিয়েছিল ; সুতরাং গণনার আবশ্যকতা নিশ্চয়ই অনুভূত হয়েছিল । তখনকার লোকে তামা ও কাঁসার পাত্র নির্মাণের কৌশলও শিখে ফেলেছে । 

সংখ্যার ধারণা

এ অবস্থায় অবশ্যই ভাষা গঠনও প্রয়োজন হয়েছিল কিন্তু তখনও সংখ্যার ধারণা বেশ অস্পষ্ট ছিল ; সংখ্যাগুলো সর্বদাই বস্তুর সঙ্গে সংশ্লিষ্ট থাকত— যেমন পাখীটা , একজোড়া জানোয়ার এক হাঁড়ি মাছ, দুটো হাত, মানুষগুলো, অনেক গাছ , সাতটা তারা ইত্যাদি । অন্ততঃ অস্ট্রেলিয়া , আমেরিকা ও আফ্রিকার অনেক গোত্রই যে দুশো বছর আগেও এই অবস্থায় ছিল, সে ত প্রত্যক্ষ সত্য । মোটকথা , বস্তু-নিরপেক্ষ বিশুদ্ধ সংখ্যার ধারণা আরও পরে এসেছে । সংখ্যা নির্দেশক শব্দ অল্প কয়েকটি মাত্র ছিল । আরও বৃহৎ সংখ্যা -নির্দেশ প্রথমে শুধু যোগের সাহায্যে , তারপর ক্রমে ক্রমে গুণ ও যোগের সাহায্যে করা হত । দুটো অস্ট্রেলীয় গোত্রের উদাহরণ দেওয়া যেতে পারে ।

• মারে রিভার গোত্র : এনিয়া ( এক ), পেচেভাল ( দুই), পেচেভাল – এনিয়া (তিন ), পেচেভাল – পেচেভাল ( চার ) ।
• কামিলা রোই গোত্র : মাল ( এক ) বুলান ( দুই ) গুলিবা (তিন ) ,বুলান – বুলান (চার ), বুলান – গুলিবা ( পাঁচ), গুলিবা – গুলিবা ( ছয়) ।

পোত – নির্মাণ ও বাণিজ্য প্রসারের ফলে সংখ্যার ধারণা ক্রমশঃ স্পষ্ট হয়ে ওঠে । আমাদের বর্তমান দশমিক প্রণালীর গণনাতেও দেখা যায় , এক থেকে দশ পর্যন্তই আমাদের মূল সংখ্যা । এর সঙ্গে বাড়তি সংখ্যা যোগ করে বৃহত্তর সংখ্যার নাম রাখা হয়েছে । আবার দশকে একক ধরে দুই দশ (বিশ ), তিন দশ (ত্রিশ), চার দশ (চল্লিশ ) ইত্যাদি গুণিতক ব্যবহৃত হয়েছে যেমন , একাদশ (দশ আর এক ), বাইশ ( দুই আর বিশ ) , পঁয়ত্রিশ (ত্রিশ আর পাঁচ )ইত্যাদি । আবার পূর্ণসংখ্যক দশের থেকে একক ঘাটতি বুঝাতে ‘ ঊন ‘ ব্যবহার করা হয়েছে । যেমন ঊনচল্লিশ (এক কম চল্লিশ ), ঊননব্বই ( এক কম নব্বই ) ইত্যাদি । কোনও কোনও ক্ষেত্রে বিশেষ করে বয়স গণনায় বা টাকার গণনায় কুড়িকে একক ধরে বৃহৎ সংখ্যার গণনার রীতিও দেখা যায় যেমন , তিন কুড়ি চার ( চৌষট্টি ) টাকা ,চার কুড়ি আট ( অষ্টাশি) বছর ইত্যাদি । 

আরো পড়ুনঃ বদমাস BODMAS নিয়ম কি সঠিক ? 

আমেরিকার আদিম অধিবাসীদের মধ্যে গণনা

আমেরিকার আদিম অধিবাসীদের মধ্যে গণনা – প্রণালী অনুসন্ধান করতে করতে দুই, পাঁচ , দশ কুড়ি প্রভৃতির ভিত্তিতে গণনার নিদর্শন পাওয়া গেছে । বিশেষ করে মেক্সিকোর ‘ মায়া’দের এবং ইউরোপের ‘কেল্ট’দের বিশ -ভিত্তিক গণনা উল্লেখযোগ্য । সুমারীয় ও বাবিলনীয় ষাট – ভিত্তিক গণনাও ( ২১০০ খ্রীস্ট-পূর্ব)সবিশেষ উল্লেখযোগ্য । আমরা যে ‘ ষাট সেকেন্ডে এক মিনিট আর ষাট মিনিটে এক ঘণ্টা’ ব্যবহারে অভ্যস্ত হয়ে গেছি , এটাও প্রাচীন মেসোপটেমীয় ( সুমারীয়+ বাবিলনীয় ) সভ্যতারই অবদান।

তাছাড়া , কড়া গণ্ডা ডজন কুড়ি প্রভৃতিতে আমরা ৪ , ১৬ , ১২ , ৮০ প্রভৃতির গুচ্ছ ব্যবহার করে থাকি। ব্যবহারিক ক্ষেত্রে জিনিসের মাপ বা গণনা সংরক্ষণের জন্য রশিতে গিরে দেওয়া , বাঁশের কঞ্চি বা কাঠে দাগ দেওয়া আঁটি বাঁধা ইত্যাদির প্রচলন ছিল । চল্লিশ – পঞ্চাশ বছর আগেও আমাদের দেশে গোয়ালের দুধের হিসাব রাখার জন্য ফাড়া কঞ্চির ব্যবহার ছিল ।দুই ভাগে ফাড়া কঞ্চি একত্র করে সংযোগ স্থলের উপর ধারাল কাচি দিয়ে দাগ কাটা হত , তারপর ক্রেতা আর বিক্রেতা দুই জনের কাছেই ওর এক এক অংশ থাকত , যাতে একজন অতিরিক্ত দাগ কেটে অপরকে ঠকাতে না পারে । ওতে সের পোয়ার হিসাব থাকত , পাঁচ সেৱ , দশ সেরেরও আলাদা চিহ্ন থাকত । এই প্রকার রীতি যে অতি প্রাচীনকাল থেকেই এমনকি , নতুন প্রস্তরযুগেও প্রচলিত ছিল তার প্রমাণ পাওয়া গেছে ১৯৩৭ সালে মোরাডিয়ার অন্তর্গত ভেস্টোনিস অঞ্চলে । 

দৈর্ঘ্যের মাপ

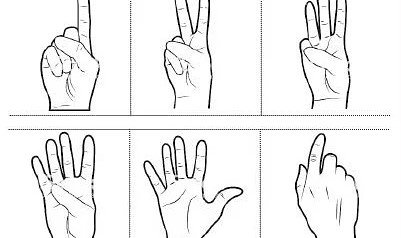
ঐ স্থান খনন করে নেকড়ের সামনের পায়ের সাত ইঞ্চি লম্বা একখণ্ড হাড় ( Radius ) পাওয়া গেছে , যাতে পঞ্চান্নটা গভীর আড়াআড়ি দাগ কাটা রয়েছে— প্রথম পঁচিশটি দাগ পাঁচ থাকে পর পর সাজান ; তারপর দুটো বড় বড় সমাপ্তি রেখা অবশিষ্ট ত্রিশটি দাগকে পৃথক করে দিয়েছে ; এরপর বাকি ত্রিশটা দাগও পাঁচ পাঁচটি করে হয় থাকে সাজান রয়েছে । এর থেকে মনে হয় , হাতের আঙ্গুল গুনতে গুনতেই যে প্রথম গণনার সূত্রপাত হয়েছে , তা ঠিক না – ও হতে পারে । 

কারও কারও মতে , হাতের আঙ্গুল গুনে সংখ্যার হিসাব , কোনও বিশেষ সামাজিক অবস্থায় আরম্ভ হয়েছিল । দশ এবং পাঁচের গুণ ও যোগ -বিয়োগের সাহায্যে সংখ্যা গণনার এই দ্বৈধ দৃষ্টান্ত কয়েক হাজার বছর ধরে প্রাচীন মিসর এবং সিন্ধু নদের অববাহিকা মহেঞ্জোদারোতে চালু ছিল ।

দৈর্ঘ্যের মাপে হাত , ফিট ( পা ) , রশি , অঙ্গুলি , নল ( পোল ) সুত ( সুত্র , সুতা ) প্রভৃতির সঙ্গে কৃষিকার্য গৃহ নির্মাণ , বস্ত্র- বয়নের সম্পর্ক লক্ষ্য করা যায় ওজনের মাপে গ্রাম ( ছোলা ) , তিল , রতি ( কুঁচের ওজন ) মেন ( দানা ) আয়তনের মাপে সের ( পাত্র বিশেষ ) , কাঠা ( পাত্র বিশেষ ) মৌটি (তৈলাদি মাপক হাতলওয়ালা ক্ষুদ্র বাটি ) প্রভৃতির সঙ্গে ব্যবহারিক সম্পর্ক রয়েছে । এই পরিমাণগুলো নিয়েই পরিমিতির প্রথম সূত্রপাত হয়েছিল ।

ম্যাজিক সংখ্যা

ইতিপূর্বেই মৃৎ -শিল্প এবং মূর্তি সম্বন্ধে উল্লেখ করা হয়েছে , এর থেকে দেখা যায় , প্রতিসাম্য সাদৃশ্য ও সর্বসমতার সঙ্গে সৌন্দর্যের সম্পর্কের কথা সুদূর অতীতেই লোকের মনে উদয় হয়েছে অতীত যুগের ধর্মীয় উৎসব ও চিকিৎসাদি ব্যাপারে টোটকা , তাবিজ ; যুদ্ধ প্রভৃতির ভিতর দিয়ে স্বস্তিক , ক্রুশ ত্রিভুজ , চতুর্ভূজ , পঞ্চফলক এবং ১ ৩ , ৫ , ৭ , ৯ প্রভৃতি ম্যাজিক সংখ্যার প্রতিও মানুষের দৃষ্টি আকৃষ্ট হয়েছিল ।

অতি প্রাচীনকাল থেকেই চন্দ্র , সূর্য , তারকাদির গতি লক্ষ্য করে সময় নির্ধারণের চেষ্টা চলছিল। খেত – খোলা এবং ব্যবসায় – বাণিজ্যের প্রসারের সঙ্গে সঙ্গে এগুলো বৈজ্ঞানিক পর্যবেক্ষণের বিষয় হয়ে পড়ল । মানবেতিহাসের অনেক গোড়ার দিকেই চান্দ্র বার্ষিক পঞ্জিকার প্রচলন দেখা যায় । আদিম যুগের মানুষও উত্তরায়ণ দক্ষিণায়ন ও সপ্তর্ষি মণ্ডলের আবির্ভাব স্থান লক্ষ্য করে বৎসরের ঋতু নির্ণয় করতে পারত । কোনও কোনও দেশের লোক নক্ষত্রমণ্ডলী লক্ষ্য করে সমুদ্র পথে দিক নির্ণয়ে দক্ষতা অর্জন করেছিল । এইসব নাক্ষত্রিক পর্যবেক্ষণ থেকে গোলকের উপরকার কৌণিক দূরত্ব এবং ক্ষুদ্র বৃত্ত ও বৃহৎ বৃত্তের ধারণার প্রথম উদ্ভব হয় ।